| Limits |
Nov. 28, 2024, 6:46 p.m.
Definition
Limits
-> the f(x) is defined when x is near the number a.
-> it must be on interval that contains x = a, except possibly at x = a.
Symbol:
![]()
Where:
The limit of f(x), as x approaches a, equals L.
One - Sided Limits
-> the left - hand/right - hand limit of f(x) as x approaches a is equal to L if can make the values of f(x) arbitrary close of L by taking x to be sufficiently close to a with less/greater than a.
Symbol:
![]() and
and ![]()
Infinite Limits
-> let f be a function defined on both sides of a, except possibility at a itself.
Symbol:
![]() and
and ![]()
Where:
The values of f(x) can be arbitrarily large positive or negative by taking x sufficiently close to a, but not equal to a.
Laws of Limit |
1. Sum Law
-> the limit of a sum is the sum of the limits.
Formula:
![]()
2. Difference Law
-> the limit of a difference is the difference of the limits.
Formula:
![]()
3. Constant Multiple Law
-> the limit of a constant times a function is the constant times the limit of the function.
Formula:
![]()
4. Product Law
-> the limit of a product is the product of the limits.
Formula:
![]()
5. Quotient Law
-> the limit of a quotient is the quotient of the limits and must not the denominator be 0.
Formula:
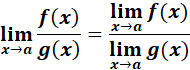
6. Power Law
-> the Ln for every positive integer n.
Formula:
![]()
7. Root Law
-> the expressions involving radicals (roots) when taking the limit as the variable approaches a particular value.
Formula:
![]()
Example |
1. Find the answer from this given:
![]()
Steps:
a. Use the law limits. Must be the following: Sum, Difference, and Constant Multiple.
b. Substitute the x.
c. Compute.
= ![]()
= ![]()
= ![]()
= 2(5)2 - 3(5) + 4
= 39
Exercises |
1. ![]()
Steps:
a. Use the law limit.
b. Substitute the x.
c. Compute.
Solution:
= ![]()
= Formula: ![]()
= ![]()
= 3 . 3
= 9
Answer: 9
2. ![]()
Steps:
a. Use the law limit.
b. Substitute the y.
c. Compute.
Solution:
= ![]()
= Formula: ![]() ;
;
![]()
= ![]()
= (-2)3 + 5(-2) - 1
= -19
Answer: -19
3. 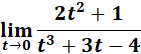
Steps:
a. Use the law limit.
b. Substitute the t.
c. Compute.
Solution:
= 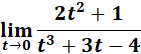
= Formula: ![]() ;
;
![]()
= Denominator: ![]()
= 03 + 3(0) - 4 = -4
= Nominator: ![]()
= 2(02) + 1 = 1
= ![]()
Answer: ![]()
4. 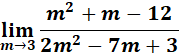
Steps:
a. Use the law limit.
b. Substitute the m.
c. Factor out and cancel to reduce.
d. Compute.
Solution:
= 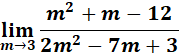
= Formula: ![]() ;
;
![]()
= 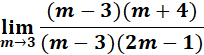 ;
; 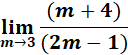
= Denominator: ![]()
= 2(3) - 1 = 5
= Nominator: ![]()
= 3 + 4 = 7
= 7/5
Answer: 7/5
5. 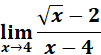
Steps:
a. Use the law limit.
b. Substitute the x.
c. Rationalize the numerator by denominator.
d. Compute.
Solution:
= 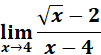
= Formula: ![]() ;
;
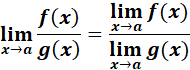
= 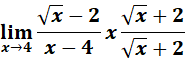
= 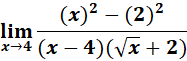
= 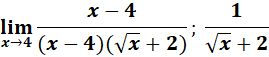
= 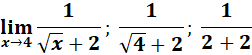
= 1/4
Answer: 1/4
